Grid from Points
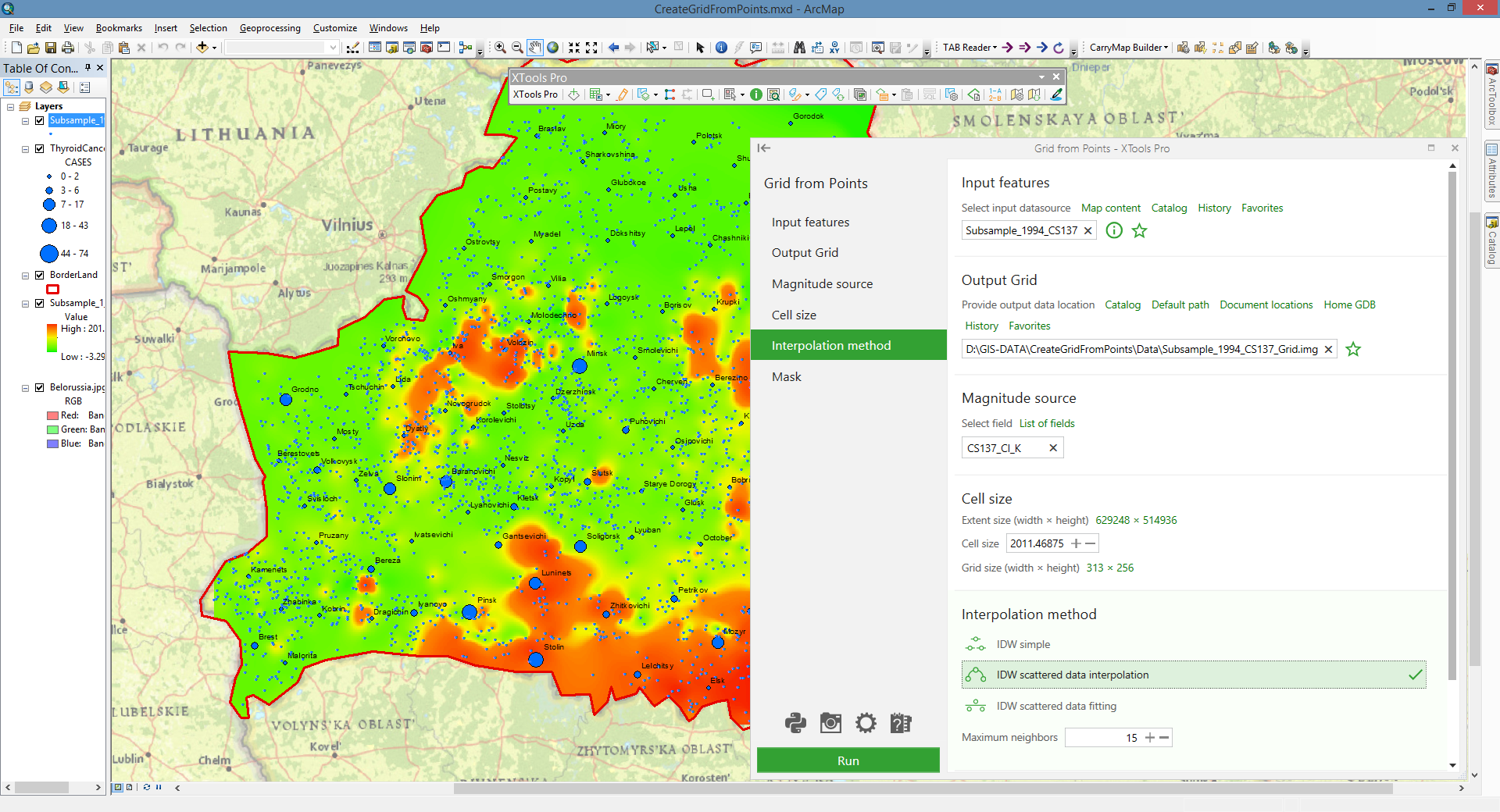
Creates grids from point data interpolating input points by values from selected attribute field.
 Available in XTools Pro for ArcMap and for ArcGIS Pro
Available in XTools Pro for ArcMap and for ArcGIS Pro
The tool is provided for creating grids from point features, i.e. interpolating point by values from the selected attribute field.
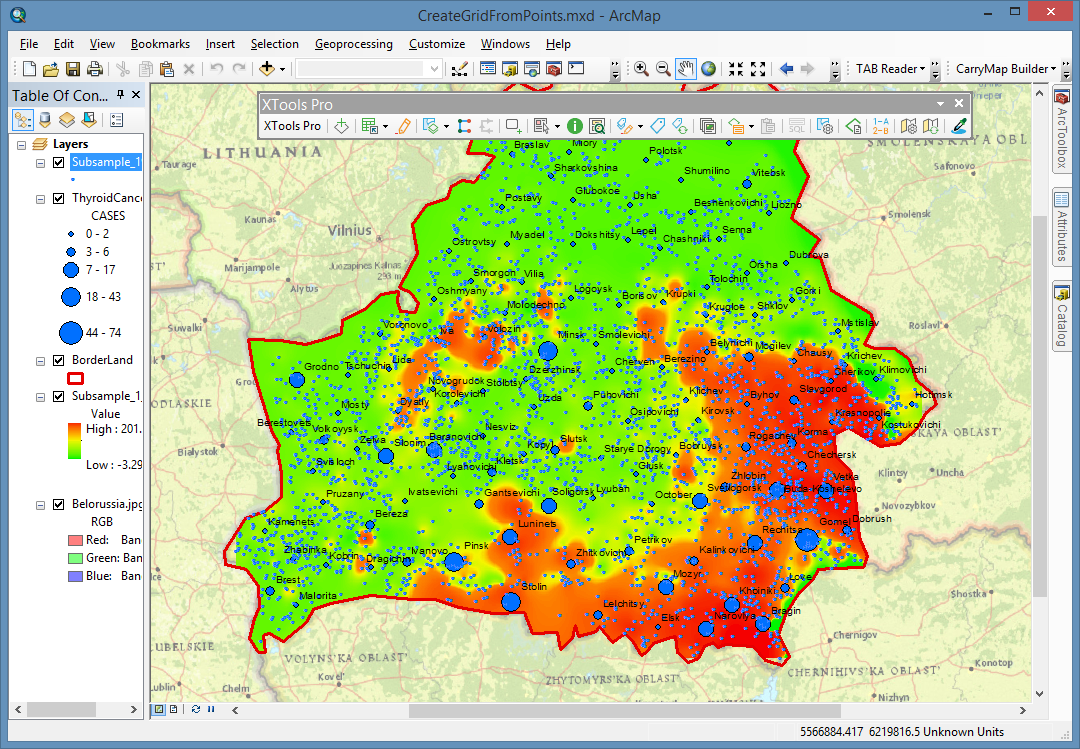
Grid is a geographic representation of the world as an array of cells arranged in rows and columns. Each grid cell is referenced by its geographic X, Y location. Raster cell is a discretely uniform unit (square or rectangle) that represents a portion of the earth such as a square meter or square mile. Each pixel has a value that corresponds to the feature or characteristic at that site such as a soil type, census tract, or vegetation class.
With the “Grid from Points” tool you can create grids from point data interpolating input points by the specified field values.
Specifying output grid parameters
To specify grid, define the size of its cells in input layer units. Grid width and height are calculated (rounded values used) depending on the specified cell size.
Define output grid format and location. Supported for grid storing formats are Esri GRID, ERDAS IMAGINE and TIFF.
Specifying interpolation parameters
The input points are interpolated using inverse distance weighting (IDW) algorithms:
IDW simple
The simplest form of inverse distance weighting interpolation. Simple and fast, this algorithm may show lower performance on large datasets, gives too much weight for distant nodes and is too sensitive to distant outliers. f(x) is flat at the interpolation nodes, i.e. it has zero derivative at the nodes.
IDW scattered data interpolation
This modified algorithm is able to interpolate scattered data and provides good performance even for large datasets. Other advantages are - absence of "flat spots" near interpolation nodes, locality of interpolation algorithm, f(x) depends only on nearest neighbors of x which significantly improves quality of interpolation, ability to work with noisy data. At that, the following drawbacks can be mentioned - it is faster than original IDW algorithm only for large datasets (hundreds of points and more), in some rare cases f(x) may have discontinuities.
IDW scattered data fitting
This algorithm is modified to fit noisy data and should be applied only to noisy tasks. In absence of noise it has no benefits over interpolation algorithm.
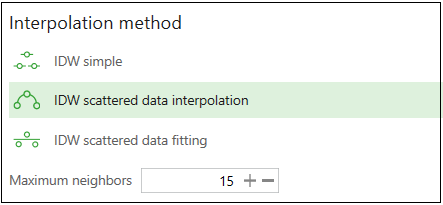
Maximum neighbors
This parameter defines the maximum number of neighboring points taken into account for interpolating a value in an unmeasured location.
 Paid tool.
Paid tool.